RANGKAIAN HAMBATAN JEMBATAN WHEATSTONE

Ada lho sobat rangkaian hambatan yang tidak bisa ditentukan hambatan penggantinya kalau cuma dengan rumus susunan hambatan seri maupun pararel. Rangkaian hambatan ini disebut dengan Wheatstone Bridge atau jembatan wheatstone. Rangkaian ini digunakan utuk menyederhanakan susunan hambatan yang pada awalnya tidak dapat disederhankan secara pararel maupun seri. Ada cerita menarik dibalik sejarah Wheatstone. Ternyata jembatan wheatstone tidak ditemukan oleh Sir Charles Wheatstone melainkan oleh Samuel Hunter Cristie pada tahun 1833. Dinamakan wheatstone karena yang berperan besar mempopulerkan rangkaian ini adalah Sir Charles Wheatstone.

Gambar di bawah ini meski bentuknya aga berbeda tapi sejatinya sama. Gambar tersebut merupakan susunan jembatan Wheatstone.

3 rangkaian sama tapi bentuk berbeda

Bagiaman Menentukan Hambatan Pengganti?

Untuk mendapatkan besarnya hambatan pengganti pada susunan hambatan jembatan Wheatstone sobat bisa menggunakan aturan dan rumus berikut:

1. Apabila perkalian silang antara R1 dan R3 sama dengan R2 dan R4 maka R5 (hambatan yang ditengah) dapat diabaikan sehingga sobat tinggal menjumlah secara seri kemudian dipararelkan.

Hambatan di Tengah Ditiadakan

Setelah hambatan tengah dianggap tidak ada gunakan prinsip seri-pararel untuk menmukan besarnya hambatan pengganti.

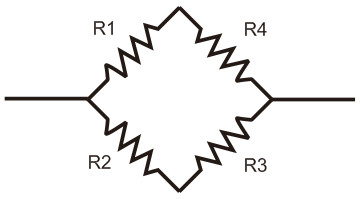
2. Jika perkalian silang antar R1 dan R3 tidak sama dengan perkalian antara R2 dan R4,  maka hambatan itu harus diganti dengan hambatan baru sehingga susunan hambatannya menjadi seperti tampak pada gambar di bawah ini.

Henggantian Hambatan (amati letak Ra, Rb, dan Rc)

Keterangan
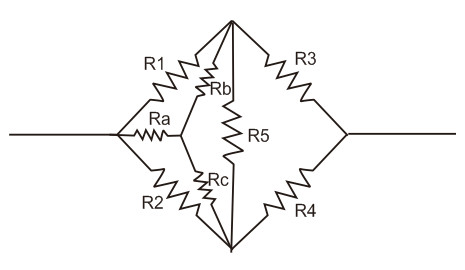
R1, R2, dan R5 masing-masing diganti dengan Ra, Rb, dan Rc. Sehingga susunan menjadi tampak seperti gambar di bawah ini.

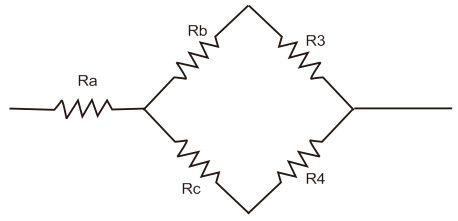
Rumusnya
R_a = R₁ . R₂ / (R₁ + R₂ + R₂)
R₂ = R₁ . R₅ / (R₁ + R₂ + R₂)
R₃ = R₂ . R₅ / (R₁ + R₂ + R₂)

Selanjutnya sobat tinggal melanjutkan dengan prinsip seri dan pararel hambatan untuk menemukan berapa hambatan penggantinya. Biar tidak bingung, yuk simak contoh soal dan pembahasan berikut ini.

Contoh Soal Jembatan Wheatstone 1

Soal 1

Amati gambar di atas. Jika diketahui v yang mengalir dari ujung kiri ke ujung kanan adalah 15 volt. Hitunglah kuat arus yang melalui rangkaian tersebut
Jawab
dari gambar di atas
R₁ . R₃ = R₂ . R₄
5 . 10 = 5 . 10
sehingga R 5 tidak perlu kita anggap.
R₁ dan R₄ (dirangkai seri)
R₁₄ = R₁ + R₄ = 5 + 5 = 10 Ω
R₂ dan R₃ (dirangkais seri)
R₂₃ = R₂ + R₃ = 10 + 10 = 20 Ω
R14 dan R23 (dirangkai pararel)
1/R_total = 1/R₁₄ + 1/R₂₃
1/R_total = 1/₁₀ + 1/₂₀
1/R_total = 2/20 + 1/20 = 3/20
1/R_total  = 30/3 =  20/3 Ω
Besarnya kuat arus yang mengalir
I = V/Rtotal = 15x 3/20 = 2,25 Ampere
Jadi dari soal jembatan wheatstone tersebut bisa jawab besarnya arus yang mengalir dalam rangkaian adalah 2,25 A.

Contoh Soal Jembatan Wheatstone 2

Amati gambar diatas dan tentukanlah berapa besar hambatan penggantinya!
Jawab
R₁. R₄ ≠ R₂. R₃
Sehingga hambatan-hmbatan tersebut perlu diganti sehingga menjadi
R_a = (2×4) / (2+4+2) = 8/8 = 1 Ω
R_b = (2×2) / (2+4+2) = 4/8 = 0,5 Ω
R_c = (4×2) / (2+4+2) = 8/8 = 1 Ω
(sobat perhatikan urutan perkaliannya)
Sekarang rangkaiannya akan tampak seperti gambar di bawah ini.
R_b dan R₂ (dirangkai seri)
R_b2 = R_b + R₂ = 0,5 + 1,5 = 2 Ω
R_c dan R₄ (dirangkai seri)
R_c4 = R_c + R₄ = 1 + 1 = 2 Ω
R_b2 dan R_c4 (dirangkai pararel)
1/R_b2c4 = 1/2 + 1/2
1/R_b2c4 = 1
R_b2c4 = 1Ω
Ra dan R_b2c4 (dirangkai seri)
R_total = Ra + R_b2c4
R_total = 1 + 1 = 2 Ω
Jadi dari soal jembatan wheatstone tersebut bisa jawab besarnya hambatan pengganti adalah 2 Ω

Copas dari : http://rumushitung.com/2014/08/30/rangkaian-hambatan-jembatan-wheatstone/